- Topic1/3
29k Popularity
11k Popularity
15k Popularity
6k Popularity
14k Popularity
- Pin
- 🎉 Gate Square Growth Points Summer Lucky Draw Round 1️⃣ 2️⃣ Is Live!
🎁 Prize pool over $10,000! Win Huawei Mate Tri-fold Phone, F1 Red Bull Racing Car Model, exclusive Gate merch, popular tokens & more!
Try your luck now 👉 https://www.gate.com/activities/pointprize?now_period=12
How to earn Growth Points fast?
1️⃣ Go to [Square], tap the icon next to your avatar to enter [Community Center]
2️⃣ Complete daily tasks like posting, commenting, liking, and chatting to earn points
100% chance to win — prizes guaranteed! Come and draw now!
Event ends: August 9, 16:00 UTC
More details: https://www
- #Gate 2025 Semi-Year Community Gala# voting is in progress! 🔥
Gate Square TOP 40 Creator Leaderboard is out
🙌 Vote to support your favorite creators: www.gate.com/activities/community-vote
Earn Votes by completing daily [Square] tasks. 30 delivered Votes = 1 lucky draw chance!
🎁 Win prizes like iPhone 16 Pro Max, Golden Bull Sculpture, Futures Voucher, and hot tokens.
The more you support, the higher your chances!
Vote to support creators now and win big!
https://www.gate.com/announcements/article/45974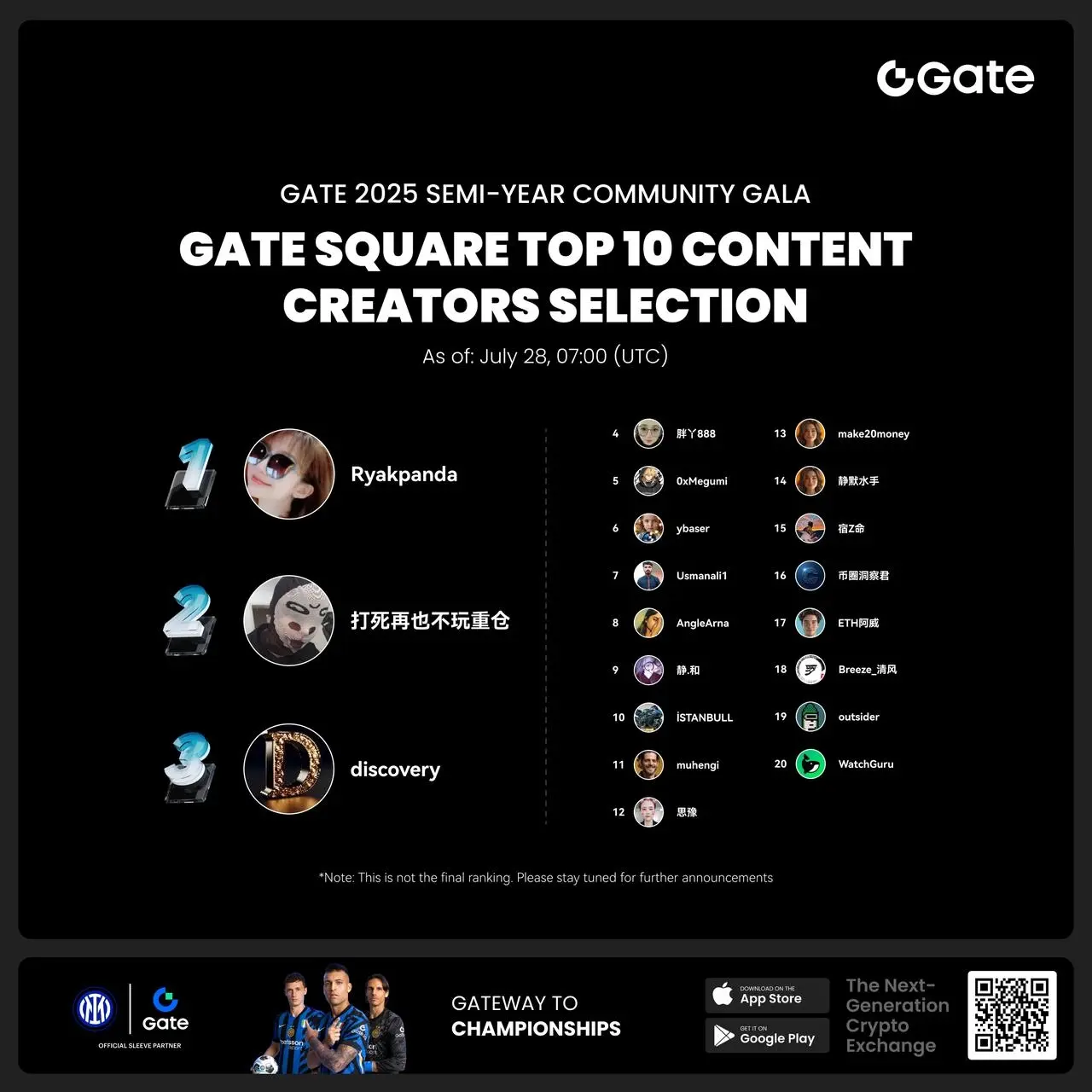
DEX Trading Operators: Efficiency and Value Trade-offs of Linear vs. Non-linear
Discussion on DEX Trading Operators: Trade-offs Between Linear and Non-linear
When developing the decentralized exchange (DEX), designing trading operators is one of the core tasks. These operators can be linear or nonlinear, similar to the distinction found when designing interest rate operators. However, this distinction is not something that everyone can easily understand.
Linear operators are usually based on the theory of equilibrium prices, assuming that the no-arbitrage condition holds. In this case, reasonable financial transactions should be linear. If non-linear results occur, they may lead to unpriceable asset combinations or the existence of arbitrage opportunities. In principle, trading models using oracle should adopt linear trading operators; otherwise, they may be subject to arbitrage. From another perspective, in a complete market and under efficient pricing, only linear trading operators can ensure no arbitrage.
However, linear operators also have their limitations. They imply that all liquidity pools are equal, and this operator cannot be tokenized because it is identical after replication. This raises the issue of capturing value and tokenization on-chain. If linear transformations are only made on existing equilibria, it is difficult to capture value.
In contrast, nonlinear trading operators attempt to accomplish three tasks simultaneously: pricing, trading, and value crystallization (tokenization). Nonlinear operators can be designed with scale-related self-reinforcing properties to crystallize value. However, this also brings some issues: as the market gradually matures, nonlinear trading operators essentially fit linear operators in extremely small trading scales; when the market is incomplete, whether the cost and efficiency of this design are sufficient; who provides the value input for the nonlinear operators, and whether this value input will gradually diminish under the competition of linear trading operators.
Many automated market makers (AMM) adopt a fixed product trading model (such as XY=K), which is a typical scale-related nonlinear trading operator. Linear trading can only be locally simulated when the market maker's pool is large enough. If the trading target of the AMM is a complete market, its core significance lies in the effectiveness of the fitting after the scale effect.
It is worth noting that attempting to place pricing power entirely on-chain may be a misunderstanding. When the market is complete, the advantages of centralized exchanges become very apparent. Every action on-chain is the product of an auction, which significantly differs from the demand for pricing trading services. For incomplete markets, such as tail assets or new projects, the core demand should be to form prices quickly and at low cost, and to complete a larger volume of transactions.
Non-linear trading operators handle pricing and trading simultaneously, but they struggle to compete with linear trading models that accept oracles in terms of efficiency. Additionally, non-linear operators face issues with value input. In a complete market, a large number of small transactions are needed to compensate for the arbitrage losses of non-linear operators during equilibrium price fluctuations, which is quite a stringent condition.
In summary, the non-linearization of trading operators is not necessarily a valuable direction. In protocols that solidify decentralized value on-chain, non-linear trading operators may not be the best choice. However, in specific areas such as interest rate operators, due to the difficulty of arbitrage, non-linear operators still have some room for application.
Future research directions may include improving nonlinear trading operators and introducing recursive information to reduce arbitrage risk. This requires a deep analysis of the core risks behind each operator and a clear modeling of trading objectives. This approach is expected to unify all financial services under operator theory, developing more effective mathematical models and thus promoting the development of the on-chain financial world.