BTC_POWER_LA
Ainda não há conteúdo
BTC_POWER_LA
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
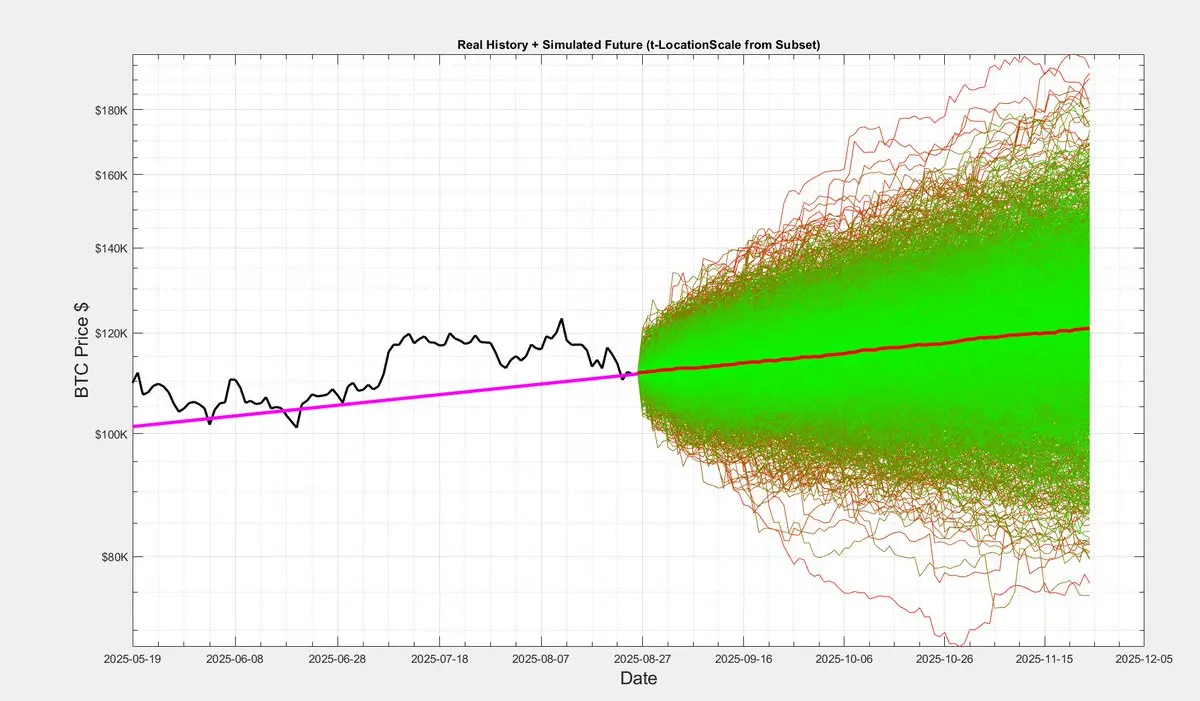
Aqui está uma prévia dos resultados da projeção da simulação de Monte Carlo para os próximos 20 anos.
Eu vou torná-lo bonito com datas e notação financeira em dólares no eixo y mais tarde.
Queria compartilhar os resultados à medida que os obtenho com vocês.
Em outras palavras, 10 M em 20 anos aqui vamos nós.
Ver originalEu vou torná-lo bonito com datas e notação financeira em dólares no eixo y mais tarde.
Queria compartilhar os resultados à medida que os obtenho com vocês.
Em outras palavras, 10 M em 20 anos aqui vamos nós.
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
Eu pedi ao Grok para explicar a importância dessas simulações de Monte Carlo.
O que nos diz sobre as leis de potência para o Bitcoin
As leis de potência são mais do que um ajuste de curva; são uma lente profunda para a evolução do BTC.
As simulações afirmam a sua relevância:
Atraentes de Longo Prazo:
A mediana (linha vermelha) abraça a extensão da lei de potência, sugerindo que é um atrator estável apesar do caos—consistente com teorias como a de Santostasi, onde n surge dos efeitos de Metcalfe da rede (valor ~ utilizadores^2, utilizadores ~ t^k).
Desvios de Curto Prazo:
Os expoentes de caud
Ver originalO que nos diz sobre as leis de potência para o Bitcoin
As leis de potência são mais do que um ajuste de curva; são uma lente profunda para a evolução do BTC.
As simulações afirmam a sua relevância:
Atraentes de Longo Prazo:
A mediana (linha vermelha) abraça a extensão da lei de potência, sugerindo que é um atrator estável apesar do caos—consistente com teorias como a de Santostasi, onde n surge dos efeitos de Metcalfe da rede (valor ~ utilizadores^2, utilizadores ~ t^k).
Desvios de Curto Prazo:
Os expoentes de caud
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
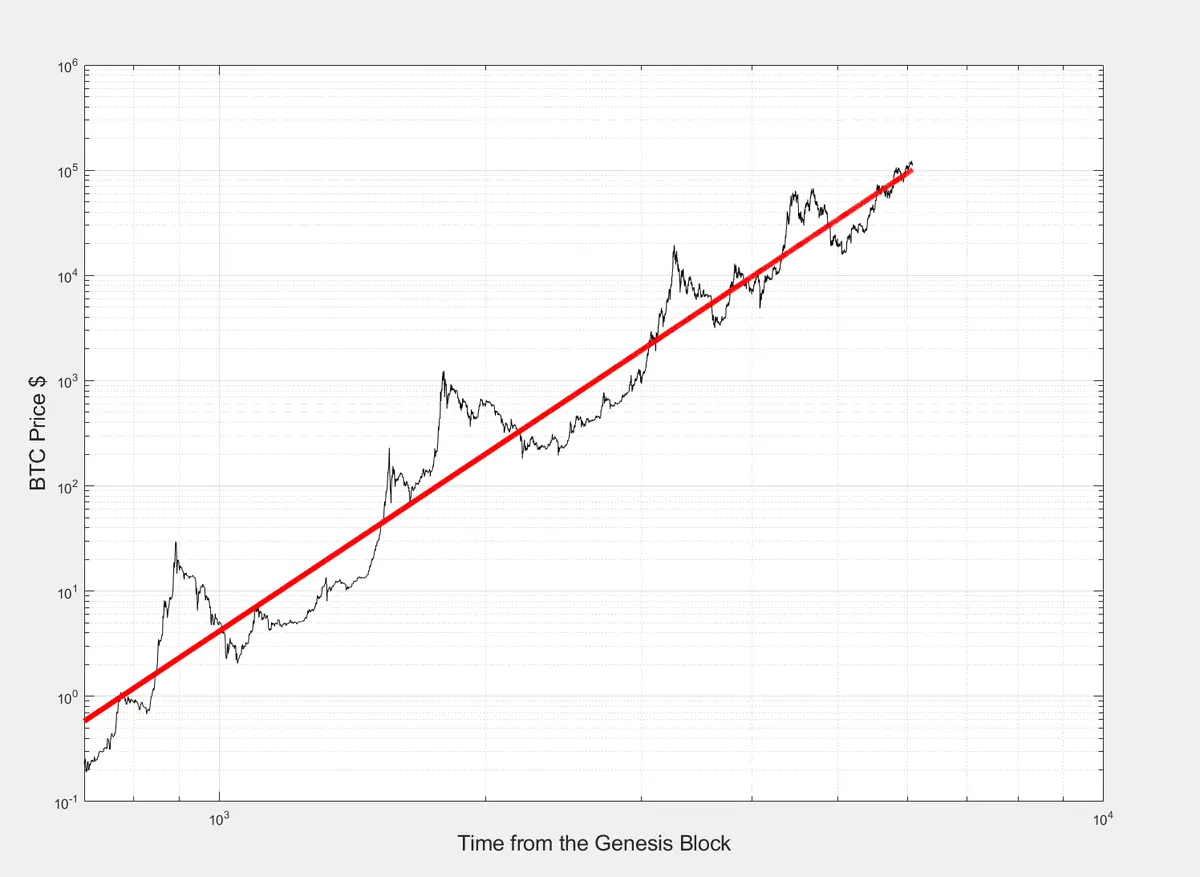
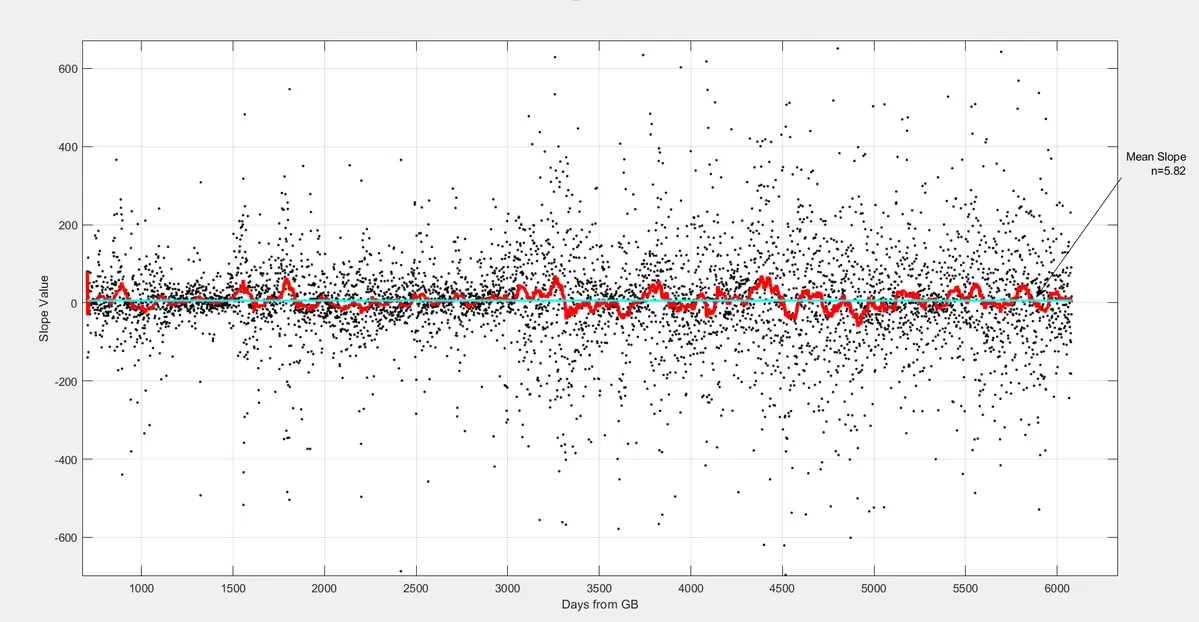
Assim, em vez de ajustar a lei de potência aos dados, você simplesmente observa que os retornos do Bitcoin decaem com o tempo.
Estas são as retornos decrescentes que frequentemente discutimos (veja o gráfico nos comentários).
Agora, consegue encontrar em vez disso uma quantidade que seja estável ( em "média" ) ao longo de toda a história do Bitcoin?
Sim, divida os retornos por t+1/t onde t é a idade do Bitcoin.
Você obtém o gráfico abaixo. É incrível como esses valores oscilam em torno de uma mediana precisa (o tipo de comportamento desses pontos de dados não tem uma média bem definida, então
Ver originalEstas são as retornos decrescentes que frequentemente discutimos (veja o gráfico nos comentários).
Agora, consegue encontrar em vez disso uma quantidade que seja estável ( em "média" ) ao longo de toda a história do Bitcoin?
Sim, divida os retornos por t+1/t onde t é a idade do Bitcoin.
Você obtém o gráfico abaixo. É incrível como esses valores oscilam em torno de uma mediana precisa (o tipo de comportamento desses pontos de dados não tem uma média bem definida, então
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
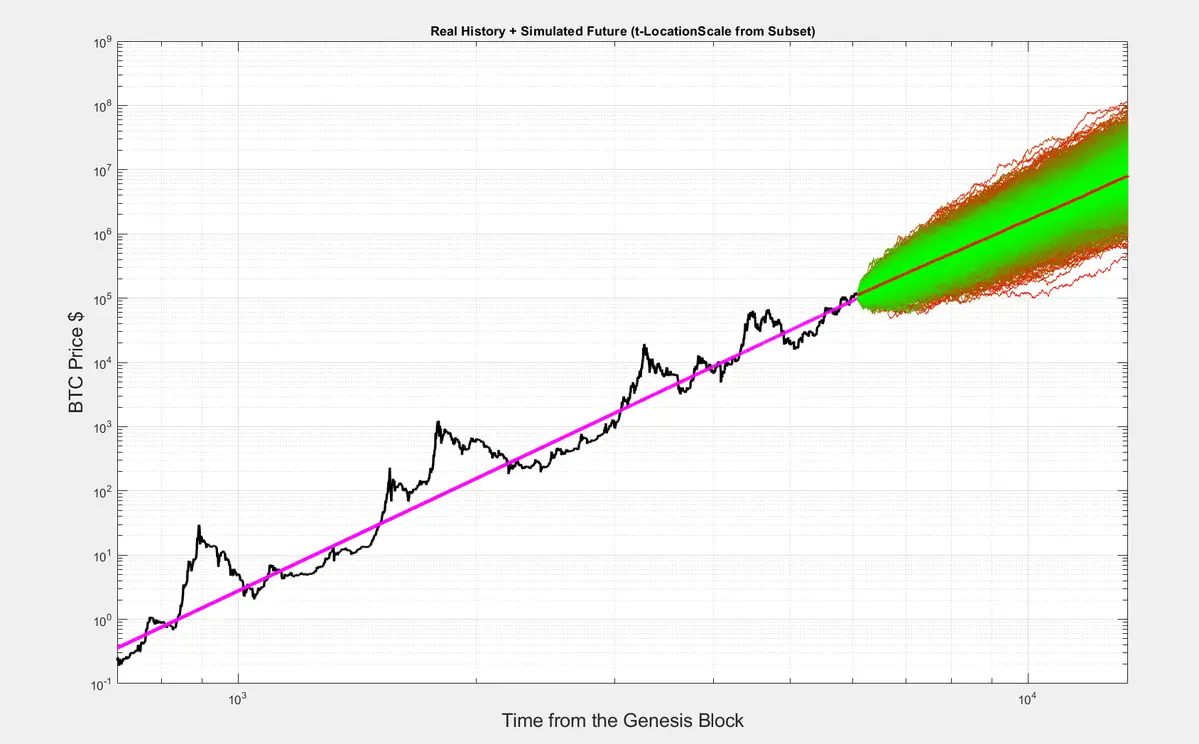
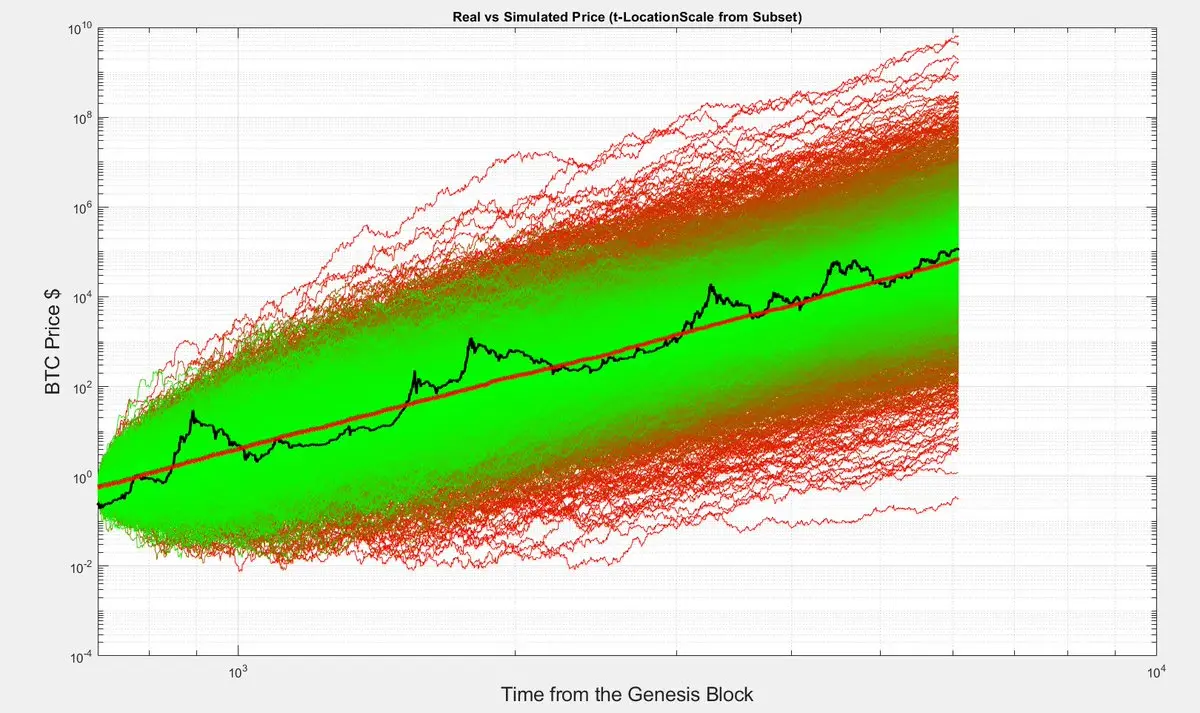
Outra forma de visualizar a simulação de Monte Carlo descrita em posts anteriores.
Aqui mostramos os caminhos individuais. As tonalidades verdes são os caminhos mais prováveis (maior densidade).
A linha vermelha é a lei de potência, mas não obtida por meio de um ajuste de regressão, mas simplesmente calculando a mediana de todos os caminhos.
Não tenho certeza se as pessoas entendem quão poderoso é este resultado.
Baseia-se em algumas suposições simples e observações empíricas:
1) O retorno observado decai com o tempo de maneira a seguir uma lei de potência: Ret=( (t+1)/t)^n, onde t é o tempo d
Ver originalAqui mostramos os caminhos individuais. As tonalidades verdes são os caminhos mais prováveis (maior densidade).
A linha vermelha é a lei de potência, mas não obtida por meio de um ajuste de regressão, mas simplesmente calculando a mediana de todos os caminhos.
Não tenho certeza se as pessoas entendem quão poderoso é este resultado.
Baseia-se em algumas suposições simples e observações empíricas:
1) O retorno observado decai com o tempo de maneira a seguir uma lei de potência: Ret=( (t+1)/t)^n, onde t é o tempo d
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
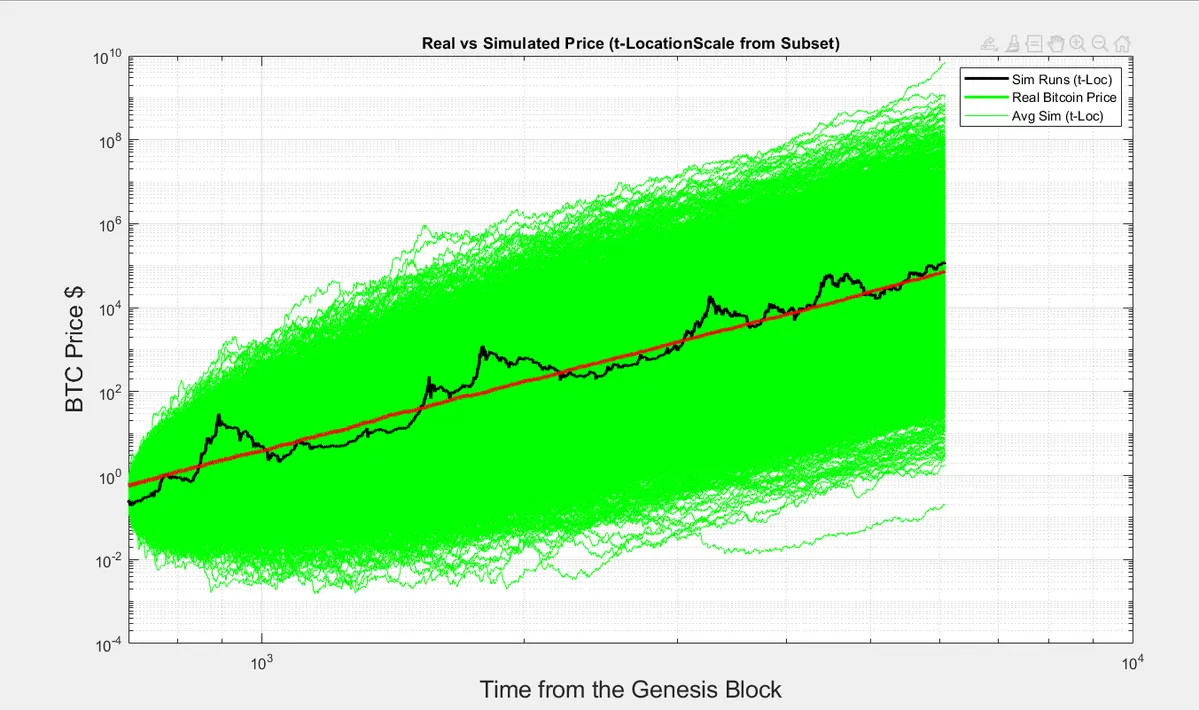
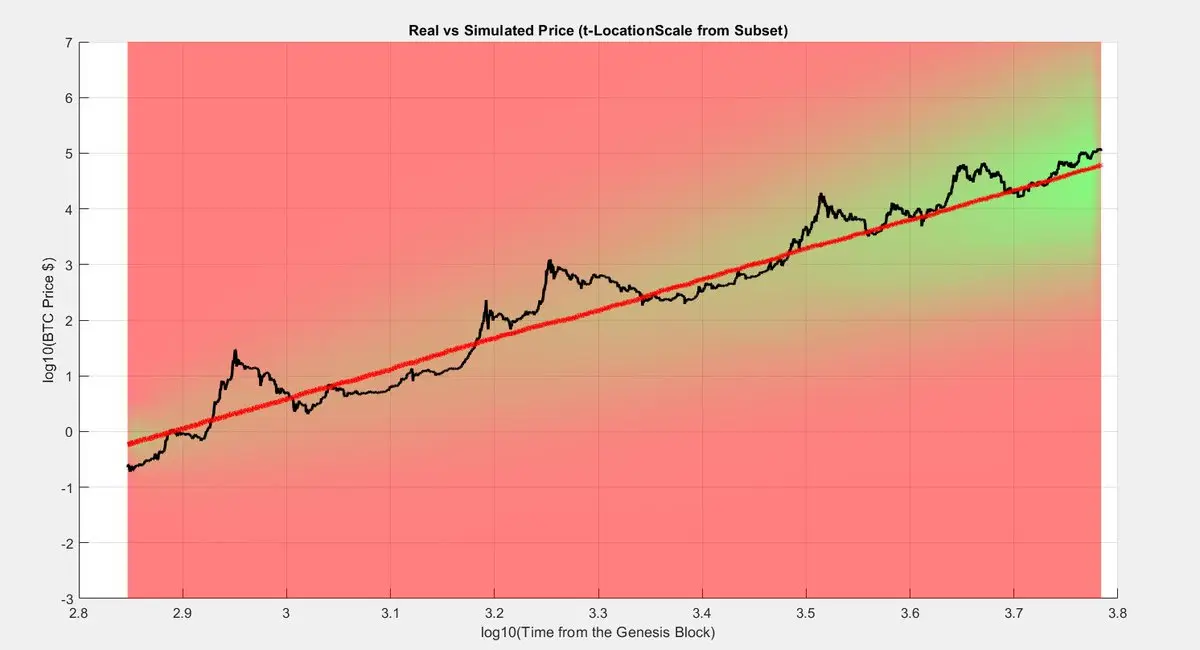
Este é o resultado de 2000 histórias virtuais de BTC usando as estatísticas observadas.
As cores na sombreamento indicam os caminhos mais prováveis, tons de verde significam mais provável.
A linha vermelha não é adequada. Isto é importante, é derivado ao tomar a mediana de todos os caminhos possíveis.
Então o Bitcoin está seguindo o caminho da menor resistência. O caminho mais provável.
Ver originalAs cores na sombreamento indicam os caminhos mais prováveis, tons de verde significam mais provável.
A linha vermelha não é adequada. Isto é importante, é derivado ao tomar a mediana de todos os caminhos possíveis.
Então o Bitcoin está seguindo o caminho da menor resistência. O caminho mais provável.
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
Grok é louco.
Eu dei estas instruções e em poucos segundos ficou feito. Provavelmente me levaria 20 minutos para criar o mesmo código.
Este é um mundo de ficção científica.
"Ok, no gráfico final onde mostramos todos os resultados, não faça a média, mas mostre os níveis de densidade dos gráficos usando tons de verde (mais denso) a vermelho (menos denso), trace as linhas para as execuções com uma linha fina cinza e sobreponha uma sombra semi-transparente baseada na densidade dessas linhas."
Ver originalEu dei estas instruções e em poucos segundos ficou feito. Provavelmente me levaria 20 minutos para criar o mesmo código.
Este é um mundo de ficção científica.
"Ok, no gráfico final onde mostramos todos os resultados, não faça a média, mas mostre os níveis de densidade dos gráficos usando tons de verde (mais denso) a vermelho (menos denso), trace as linhas para as execuções com uma linha fina cinza e sobreponha uma sombra semi-transparente baseada na densidade dessas linhas."
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
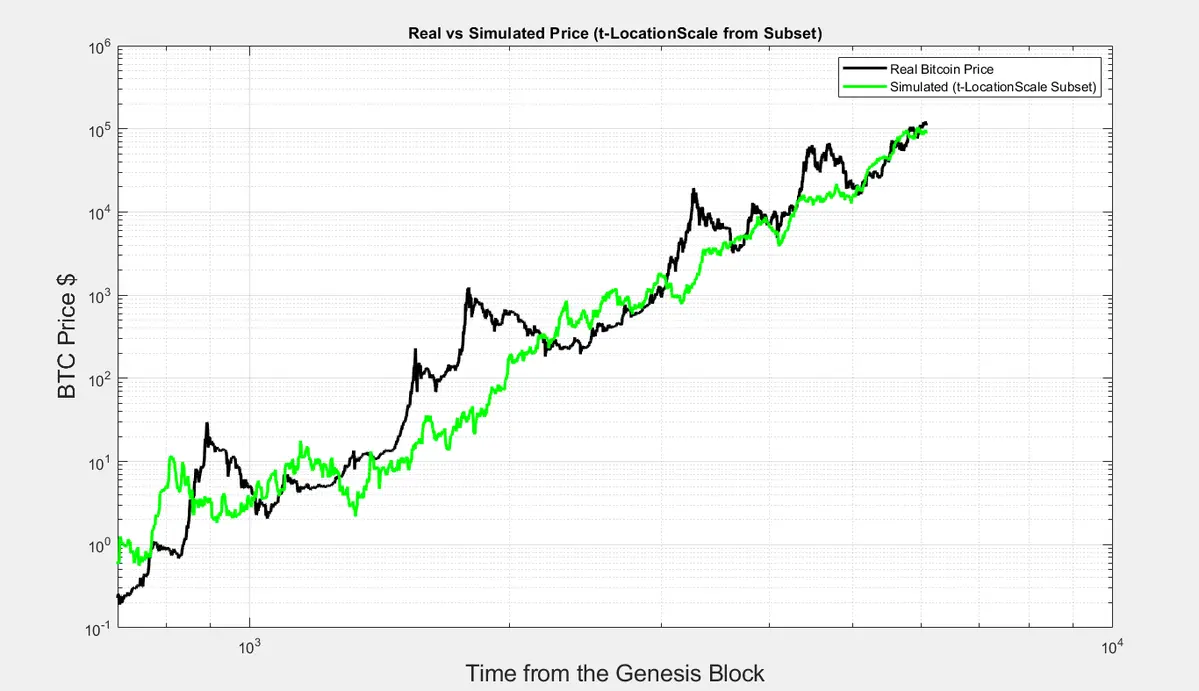
Este é um dos resultados de executar um Bitcoin completamente sintético.
Comecei com uma distribuição de modelo das inclinações ( que você pode usar uma distribuição de Lorentz ou uma distribuição t-Location Scale ) com base nos parâmetros observados.
Esta é uma distribuição invariável no tempo ( é a mesma distribuição desde o início da história do Bitcoin ).
Então podemos derivar os retornos multiplicando por um fator determinístico (não é aleatório), log(t+1/t), representando os retornos logarítmicos teóricos da lei de potência, t é o tempo desde o Bloco Gênesis.
Você então compõe os retorno
Ver originalComecei com uma distribuição de modelo das inclinações ( que você pode usar uma distribuição de Lorentz ou uma distribuição t-Location Scale ) com base nos parâmetros observados.
Esta é uma distribuição invariável no tempo ( é a mesma distribuição desde o início da história do Bitcoin ).
Então podemos derivar os retornos multiplicando por um fator determinístico (não é aleatório), log(t+1/t), representando os retornos logarítmicos teóricos da lei de potência, t é o tempo desde o Bloco Gênesis.
Você então compõe os retorno
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
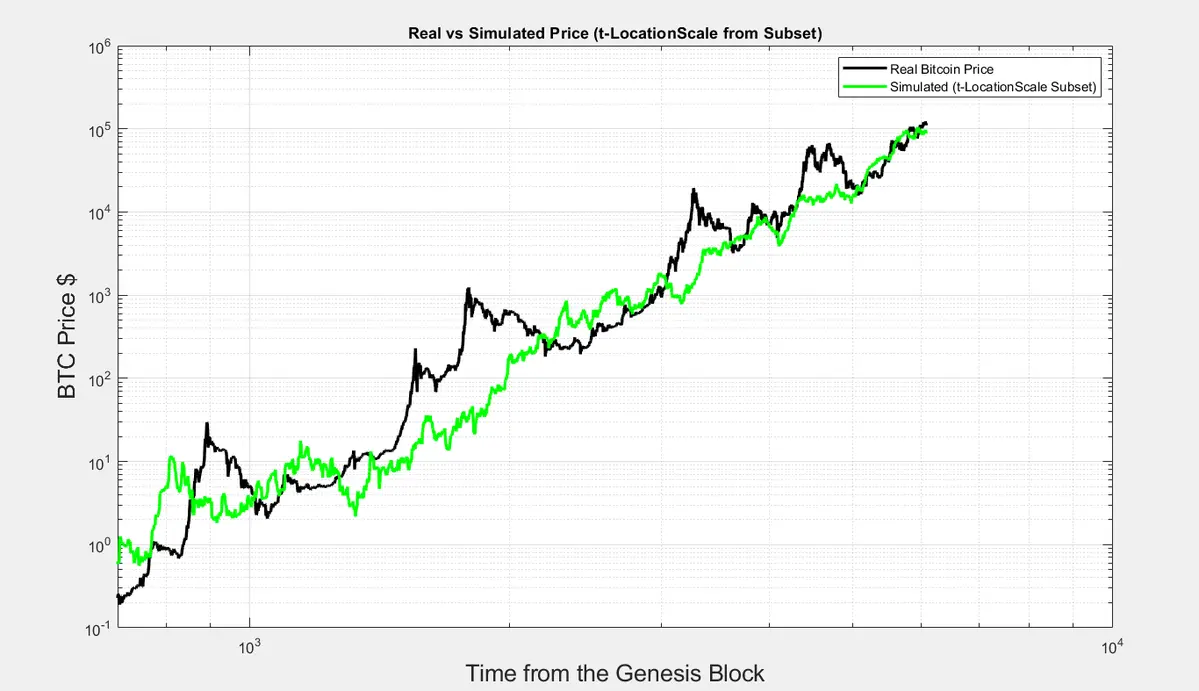
Este é um dos resultados de executar um Bitcoin completamente sintético.
Comecei com uma distribuição de modelo das inclinações ( você pode usar uma distribuição de Lorentz ou uma distribuição t-Location Scale ) com base nos parâmetros observados.
Esta é uma distribuição invariável no tempo ( é a mesma distribuição desde o início da história do Bitcoin ).
Então podemos derivar os retornos multiplicando por um fator determinístico (não é aleatório), t+1/t, representando os retornos teóricos da lei de potência, t é o tempo a partir do Bloco Gênesis.
Você então compõe os retornos ao longo do temp
Ver originalComecei com uma distribuição de modelo das inclinações ( você pode usar uma distribuição de Lorentz ou uma distribuição t-Location Scale ) com base nos parâmetros observados.
Esta é uma distribuição invariável no tempo ( é a mesma distribuição desde o início da história do Bitcoin ).
Então podemos derivar os retornos multiplicando por um fator determinístico (não é aleatório), t+1/t, representando os retornos teóricos da lei de potência, t é o tempo a partir do Bloco Gênesis.
Você então compõe os retornos ao longo do temp
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
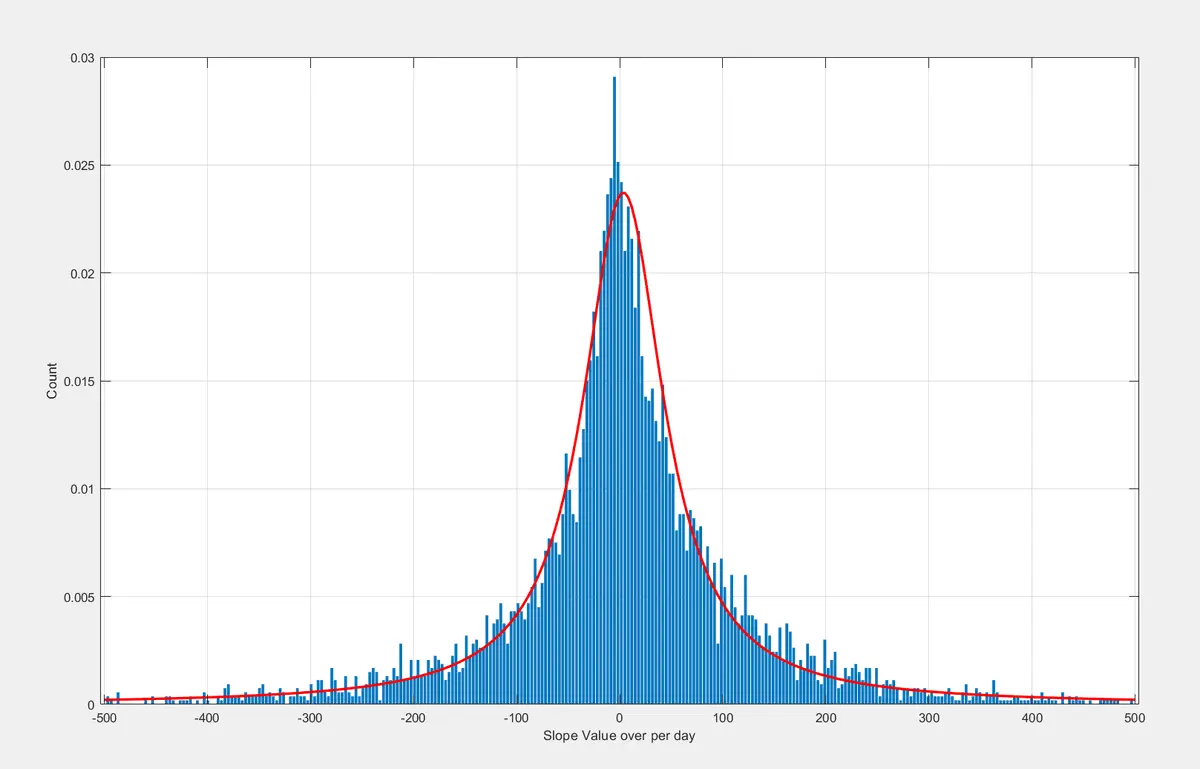
Então, a distribuição de Lorentz parece ser um bom proxy para o comportamento real. Não tenho certeza se conseguimos encontrar um melhor, deixe-me saber se você tiver sugestões.
Podemos então usar esta distribuição para recriar um preço sintético do Bitcoin e comparar a distribuição atual com a geral para nos alertar se algo mudar.
Esta é realmente a única distribuição estável que temos do Bitcoin.
Os retornos são uma função do tempo, por isso precisamos passar desta distribuição de retornos normalizados ( para retornos.
Ver originalPodemos então usar esta distribuição para recriar um preço sintético do Bitcoin e comparar a distribuição atual com a geral para nos alertar se algo mudar.
Esta é realmente a única distribuição estável que temos do Bitcoin.
Os retornos são uma função do tempo, por isso precisamos passar desta distribuição de retornos normalizados ( para retornos.
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
Às 8:15 PST teremos um novo programa "A Física do Bitcoin" com Giovanni e Stephen.
A agenda do Stephen está abaixo. Vou discutir o último gráfico da lei de potência e os meus resultados sobre a distribuição de retornos e retornos normalizados.
Por favor, junte-se a nós aqui no X, YouTube e Twitch. Links nos comentários.
Ver originalA agenda do Stephen está abaixo. Vou discutir o último gráfico da lei de potência e os meus resultados sobre a distribuição de retornos e retornos normalizados.
Por favor, junte-se a nós aqui no X, YouTube e Twitch. Links nos comentários.

- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
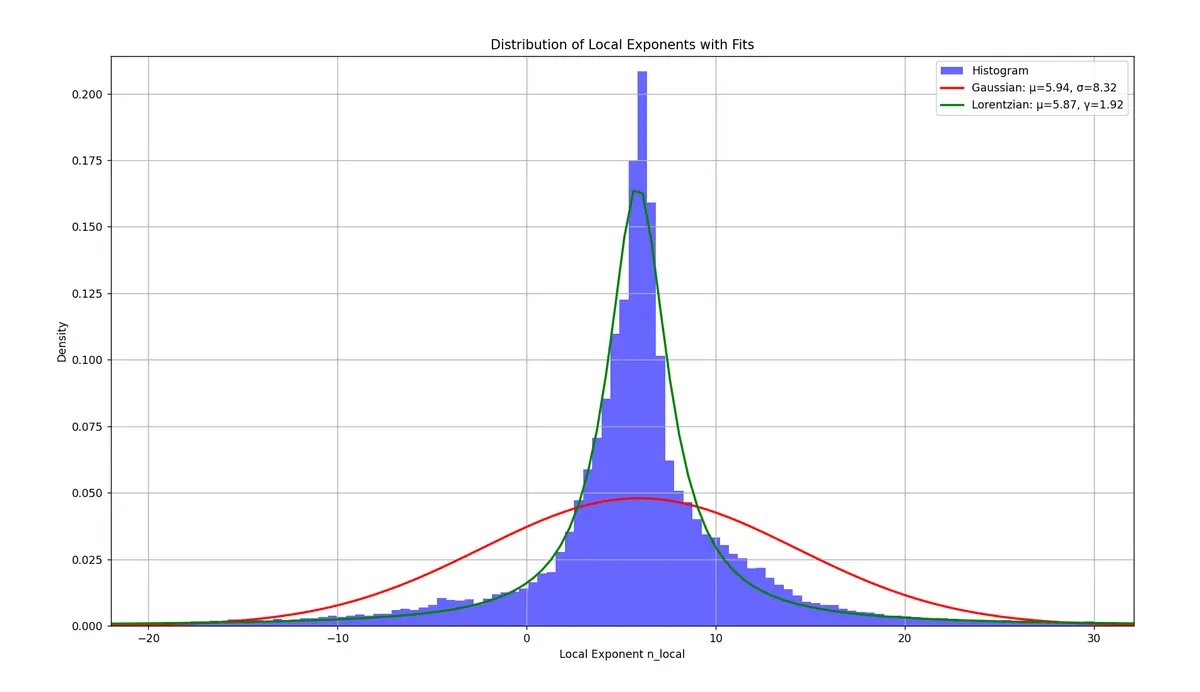
Este é realmente um gráfico fixe. Contém tudo o que você precisa saber sobre Bitcoin.
Basicamente, é um gráfico de retornos de BTC "normalizado" ao longo do tempo. Normalizamos porque os retornos são uma função do tempo, por isso dividimos pela função do tempo e deveríamos obter algo que seja estático ao longo do tempo.
É exatamente isso que obtemos e a média está em torno da inclinação da lei de potência.
Um ajuste de Lorentz é uma boa aproximação do comportamento. Provavelmente, as desvios dele são os retornos excessivos das bolhas.
Ver originalBasicamente, é um gráfico de retornos de BTC "normalizado" ao longo do tempo. Normalizamos porque os retornos são uma função do tempo, por isso dividimos pela função do tempo e deveríamos obter algo que seja estático ao longo do tempo.
É exatamente isso que obtemos e a média está em torno da inclinação da lei de potência.
Um ajuste de Lorentz é uma boa aproximação do comportamento. Provavelmente, as desvios dele são os retornos excessivos das bolhas.
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar
Não há uma única distribuição de retornos para Bitcoin, uma vez que os retornos mudam ao longo do tempo.
Os retornos são uma função do tempo:
R= (t2/t1)^n, onde n é o expoente da lei de potência.
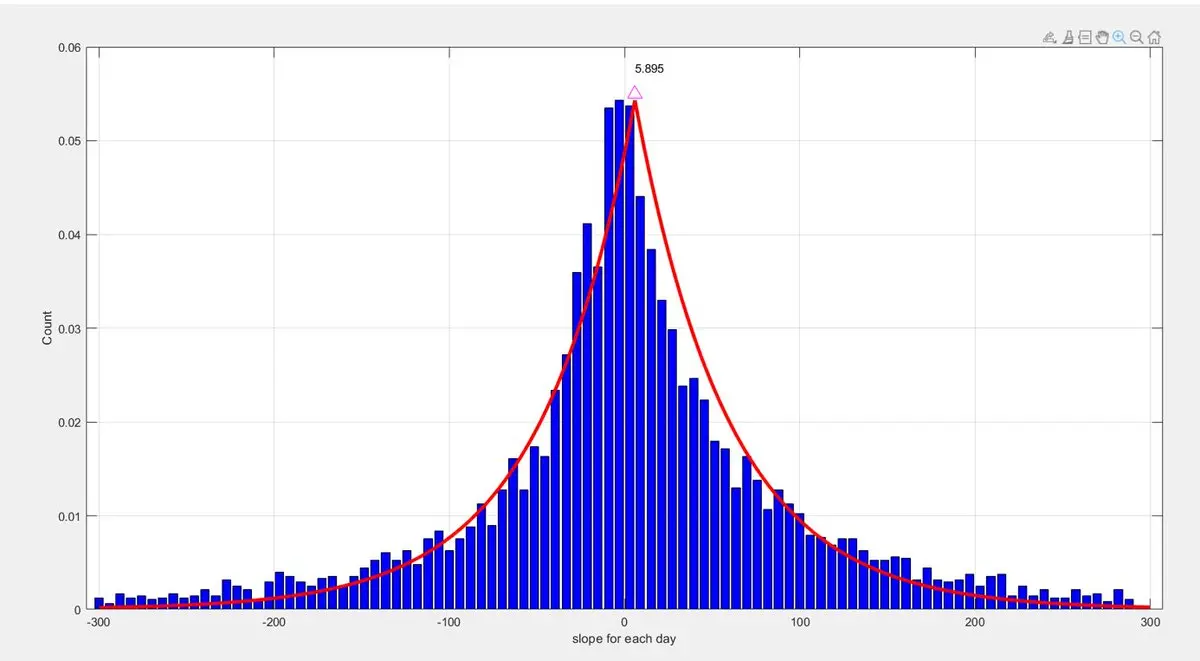
Se alguém quiser representar uma distribuição dos retornos até agora, então é melhor incluir este efeito temporal e mostrar a distribuição das inclinações.
Declives n=log(P2/P1)/log(t2/t1).
Eu mostrei que esta é uma distribuição gaussiana em torno do valor n.
Basicamente, o Bitcoin é uma lei de potência em média. Esse é um resultado profundo que mostra que a lei de potência é realmente uma propriedade
Ver originalOs retornos são uma função do tempo:
R= (t2/t1)^n, onde n é o expoente da lei de potência.
Se alguém quiser representar uma distribuição dos retornos até agora, então é melhor incluir este efeito temporal e mostrar a distribuição das inclinações.
Declives n=log(P2/P1)/log(t2/t1).
Eu mostrei que esta é uma distribuição gaussiana em torno do valor n.
Basicamente, o Bitcoin é uma lei de potência em média. Esse é um resultado profundo que mostra que a lei de potência é realmente uma propriedade
- Recompensa
- curtir
- Comentário
- Repostar
- Compartilhar